Alaw and µlaw
Introduction
Digital audio usually uses 48000 samples per second and 16‑bits per
sample, resulting in 48000 sps * 16 bits = 768000 bits per second per
channel.
Telephone systems usually use 8000 samples per second of eight bits each,
resulting in 64000 bits per second.
Reducing the sample rate can be achieved by means of a digital low pass
filter followed by re-sampling at 8000 Hz. This leaves us with the
requirement to reduce the number of bits per sample.
Alaw and µlaw are compression methods for digital audio (speech) signals.
µlaw reduces 14‑bit to 8‑bit and Alaw 13‑bit to
8‑bit. Both can also be used to reduce 16‑bit to
8‑bit.
Quantization noise
When converting an analogue signal to digital, only a limited number of
digits is used. This causes a rounding error, called quantization noise
(you can also think of it as a form of distortion though);
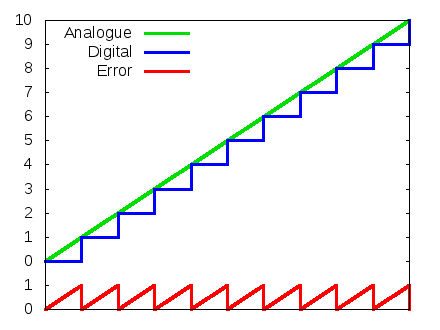
This error is never bigger than one least significant bit. So relatively
speaking this error is larger for small signals;
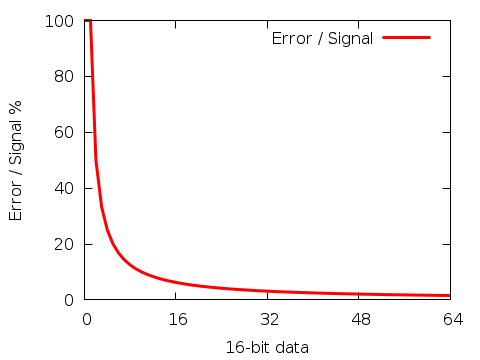
Discarding bits
Both Alaw and µlaw reduce the number of bits. They do this by discarding
(throwing away) the least significant bits. For small signals they reduce
the resolution by one bit. For slightly larger signals by two bits. Next
by three bits. Etc.
So small signals have a higher resolution than large ones. In such a way
that the relative resolution (error / signal strength) is
more or less constant;
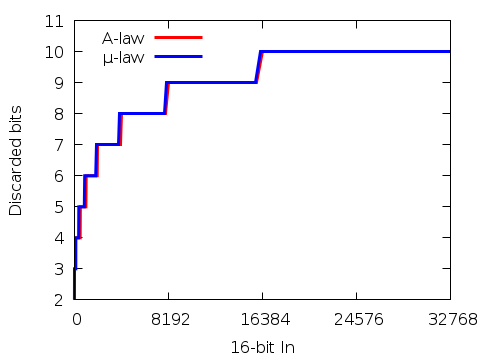
When dealing with 16‑bit signals, µlaw discards at least two bits
and Alaw at least four. And both a maximum of ten.
Below a graph representing the relationship between the signals before and
after compression for both Alaw and µlaw;
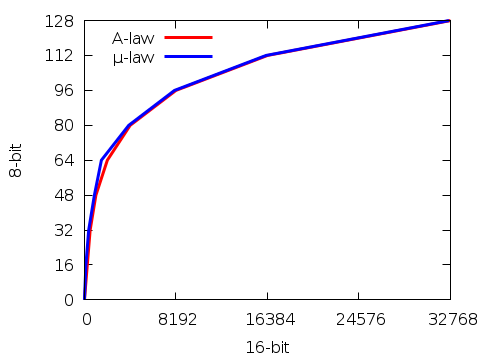
The simplest way to reduce 16- to 14‑bit is to shift the bits to the right, filling the left with zeros and discarding the rightmost bits;
xxxx xxxx xxxx xxxx 00xx xxxx xxxx xxxx
After which the data is suitable for µlaw compression.
For Alaw we just discard one bit more;
xxxx xxxx xxxx xxxx 000x xxxx xxxx xxxx
Alternatively, one can reduce the dynamic range a bit, making sure that leftmost bits are all zero.
Both Alaw and µlaw data can be thought of as 8‑bit floats. With a Sign ('s'), Exponent ('e') and Mantissa ('m'). The leftmost bit 's' is '0' for positive and '1' for negative numbers;
seee mmmm
The three 'e' bits can be '000' to '111'. If these where the rightmost bits, these would be decimal 0 to 7. But because these are in the left nibble, these are a factor 16 larger;
| Binary | Hex | Dec |
|---|---|---|
| 0000 0000 | 00 | 0 |
| 0001 0000 | 10 | 16 |
| 0010 0000 | 20 | 32 |
| 0011 0000 | 30 | 48 |
| 0100 0000 | 40 | 64 |
| 0101 0000 | 50 | 80 |
| 0110 0000 | 60 | 96 |
| 0111 0000 | 70 | 112 |
And the sign bit, being the leftmost bit, is actually 0 or 128.
Alaw
Alaw divides the input data in ranges called chords. A practical implementation may even reduce the data to 12‑bits first. This then results in the last two columns;
| Hex Exp |
Min 13-bit |
Max 13-bit |
Min 12-bit |
Max 12-bit |
|---|---|---|---|---|
| 00 | 0 | 31 | 0 | 15 |
| 10 | 32 | 63 | 16 | 31 |
| 20 | 64 | 127 | 32 | 63 |
| 30 | 128 | 255 | 64 | 127 |
| 40 | 256 | 511 | 128 | 255 |
| 50 | 512 | 1023 | 256 | 511 |
| 60 | 1024 | 2047 | 512 | 1023 |
| 70 | 2048 | 4095 | 1024 | 2047 |
Note that the boundaries are at powers of two (0, 16, 32, 64, etc).
Compression
The actual compression is rather blunt. It just keeps shifting the data to the right until the leftmost 11 bits are all zero, while keeping track of the number of shifts. This leaves us with just five bits;
0000000010101010 0000000001010101 0000000000101010 0000000000010101 ↑ 11th bit
In the table below 'x' are the discarded bits, 'a', 'b', 'c' and 'd' the bits used. These can be one or zero. The '1' left of 'abcd' is the leftmost '1' used, other than abcd. And 's' is the sign bit, which is '1' for negative numbers;
| Hex Exp |
Min In |
Max In |
Bits used | Shifts | Result |
|---|---|---|---|---|---|
| 00 | 0 | 15 | 00000000abcd | 0 | s000abcd |
| 10 | 16 | 31 | 00000001abcd | 0 | s001abcd |
| 20 | 32 | 63 | 0000001abcdx | 1 | s010abcd |
| 30 | 64 | 127 | 000001abcdxx | 2 | s011abcd |
| 40 | 128 | 255 | 00001abcdxxx | 3 | s100abcd |
| 50 | 256 | 511 | 0001abcdxxxx | 4 | s101abcd |
| 60 | 512 | 1023 | 001abcdxxxxx | 5 | s110abcd |
| 70 | 1024 | 2047 | 01abcdxxxxxx | 6 | s111abcd |
Note: Some documents show a 13- to 8‑bit compression table instead. In
these the bit after 'abcd' is always discarded. So one might as well
reduce to 12‑bits first and use the method above instead. The result is
exactly the same!
Note: The bit left of 'abcd' can be either '0' or '1'. So a total of
five bits from the original data are retained; Whenever the 'exponent'
is non-zero, the bit left of 'abcd' is '1'.
Note: These are 16‑bit integers. Because the data is reduced to
12‑bits first, the four leftmost bits are all zero. These are not shown
in the 'bits used' above.
In theory the three 'exp' bits could be used to encode seven shifts, but
Alaw uses just six.
| 0abcd | Val | 1abcd | Val |
|---|---|---|---|
| 00000 | 0 | 10000 | 16 |
| 00001 | 1 | 10001 | 17 |
| 00010 | 2 | 10010 | 18 |
| 00011 | 3 | 10011 | 19 |
| 00100 | 4 | 10100 | 20 |
| 00101 | 5 | 10101 | 21 |
| 00110 | 6 | 10110 | 22 |
| 00111 | 7 | 10111 | 23 |
| 01000 | 8 | 11000 | 24 |
| 01001 | 9 | 11001 | 25 |
| 01010 | 10 | 11010 | 26 |
| 01011 | 11 | 11011 | 27 |
| 01100 | 12 | 11100 | 28 |
| 01101 | 13 | 11101 | 29 |
| 01110 | 14 | 11110 | 30 |
| 01111 | 15 | 11111 | 31 |
For each shift multiply the value in the last column by two.
So multiply by 64 for six shifts (2⁶ = 64).
Example: '10111' with four shifts is 23 * 2⁴ = 23 * 16 = 368.
| 8-bit out | 12-bit in | 13-bit in | 16-bit in | ||||
|---|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | Min | Max |
| 0 | 15 | 0 | 15 | 0 | 31 | 0 | 255 |
| 16 | 31 | 16 | 31 | 32 | 63 | 256 | 511 |
| 32 | 47 | 32 | 63 | 64 | 127 | 512 | 1023 |
| 48 | 63 | 64 | 127 | 128 | 255 | 1024 | 2047 |
| 64 | 79 | 128 | 255 | 256 | 511 | 2048 | 4095 |
| 80 | 95 | 256 | 511 | 512 | 1023 | 4096 | 8192 |
| 96 | 111 | 512 | 1023 | 1024 | 2047 | 8192 | 16383 |
| 112 | 127 | 1024 | 2047 | 2048 | 4095 | 16384 | 32767 |
After the sign bit is added, the resulting byte is XOR-red with hex D5, which flips all the even bits and the sign bit.
Compression program
Below a small Alaw compression C program. It reads 16‑bit signed integers from stdin and writes 8‑bit unsigned integers to stdout, which can be handy for test purposes.
#include <stdio.h>
/*
* This program is free software; you can redistribute it and/or modify
* it under the terms of the GNU General Public License version 3 as
* published by the Free Software Foundation.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
* GNU General Public License for more details.
*/
int main(void)
{
unsigned char out;
short st;
int sign, cnt;
cnt = 0; /* 16 * loopcount; 0 to 7 * 16 */
out = 0; /* 8-bit out */
sign = 0; /* 128 When input negative */
st = 0; /* 16-bit in */
while (fread(&st, 2, 1, stdin) > 0) {
/* Sign */
if (st < 0) {
/* Sign is negative. Limit and change sign. */
if (st < -32767) {
/* This should not happen */
st = -32767;
}
st = st * -1;
sign = 0x80;
} else {
/* Sign is positive. */
sign = 0;
}
/* To 12 bits (plus one bit for sign is 13) */
st = st >> 4;
if ((st & 0x0ff0) == 0) {
cnt = 0;
} else {
cnt = 0x10;
while ((st & 0x0ff0) != 0x10) {
st = st >> 1;
cnt = cnt + 0x10;
/* 112 max */
if(cnt >= 0x70)
break;
}
}
/* Lower 4 bits */
st = st & 0x0f;
/* OR the lot. */
out = sign | cnt | st;
/* XOR with 1101 0101 */
out = out ^ 0xD5;
fwrite(&out, 1, 1, stdout);
}
return(0);
}
There are probably more efficient ways of doing this.
A lot of compression programs use lookup tables.
Decompression
The decompression more or less does the above in reverse order. First the data is XOR-ed with hex D5. Next a '1' is placed after the 'abcd' bit. And if the 'exponent' is not equal to zero, a '1' before 'abcd' as well. After this is done the data is shifted the appropriate number of times to the left. And if the sign bit isn't zero, the result made negative;
| In | Bits out | Shifts | Min | Max |
|---|---|---|---|---|
| s000abcd | 0000000abcd1 | 0 | 1 | 31 |
| s001abcd | 0000001abcd1 | 0 | 33 | 63 |
| s010abcd | 000001abcd10 | 1 | 66 | 126 |
| s011abcd | 00001abcd100 | 2 | 132 | 252 |
| s100abcd | 0001abcd1000 | 3 | 264 | 504 |
| s101abcd | 001abcd10000 | 4 | 528 | 1008 |
| s110abcd | 01abcd100000 | 5 | 1056 | 2016 |
| s111abcd | 1abcd1000000 | 6 | 2112 | 4032 |
During compression, the bits after 'abcd' where discarded. Now a '1' is
placed after 'abcd'. Apparently this is preferred to just appending zeros.
This means that there is no zero in the output; Its either 1 or -1.
The above output data is 13‑bit. For 16‑bit data, multiply min
and max by 8. So the full 16-bit output range is 8 to 32256. Or, including
negative numbers, -32256 to 32256.
A complete Alaw conversion table here.
µlaw
Just like Alaw, µlaw divides the input data into ranges (called chords). But unlike Alaw, the range boundaries are not neatly at powers of two; They have an offset of 33;
| Hex Exp |
Min | Max | Min +33 | Max +33 |
|---|---|---|---|---|
| 00 | 0 | 30 | - | - |
| 10 | 31 | 94 | 64 | 127 |
| 20 | 95 | 222 | 128 | 255 |
| 30 | 223 | 468 | 256 | 511 |
| 40 | 479 | 990 | 512 | 1023 |
| 50 | 991 | 2014 | 1024 | 2047 |
| 60 | 2015 | 4062 | 2048 | 4095 |
| 70 | 4063 | 8158 | 4096 | 8191 |
Compression
Zero is 'compressed' to zero.
For other values smaller than 31, add one and then divide by two. This
yields values from one to 15.
For values bigger than 30, add 33 and limit the sum to 8191 (the conversion
'clips' at 8158). Next, shift to the right twice and then process the same
way as Alaw.
| 8-bit out | 14-bit in | 16-bit in | ||||
|---|---|---|---|---|---|---|
| Min | Max | Min | Max | Min | Max | |
| 0 | 15 | 0 | 30 | 0 | 123 | |
| 16 | 31 | 31 | 94 | 124 | 379 | |
| 32 | 47 | 95 | 222 | 380 | 891 | |
| 48 | 63 | 223 | 478 | 892 | 1915 | |
| 64 | 79 | 479 | 990 | 1916 | 3963 | |
| 80 | 95 | 991 | 2014 | 3964 | 8059 | |
| 96 | 111 | 2015 | 4062 | 8060 | 16251 | |
| 112 | 127 | 4063 | 8158 | 16252 | 32632 | |
Note: Max 14-bit value is 8191, not 8158.
Note: Max 16-bit value is 32767, not 32632.
After the sign bit is added, the resulting byte is XOR-red with hex FF, which flips all the bits. This is done to avoid long sequences of zeros.
Compression program
Below a small Alaw compression C program. It reads 16‑bit signed integers from stdin and writes 8‑bit unsigned integers to stdout, which can be handy for test purposes.
#include <stdio.h>
/*
* This program is free software; you can redistribute it and/or modify
* it under the terms of the GNU General Public License version 3 as
* published by the Free Software Foundation.
*
* This program is distributed in the hope that it will be useful,
* but WITHOUT ANY WARRANTY; without even the implied warranty of
* MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
* GNU General Public License for more details.
*/
int main(int argc, char **argv)
{
unsigned char out;
short st;
int sign, cnt;
cnt = 0; /* 16 * loopcount; 0 to 7 * 16 */
out = 0; /* 8-bit out */
sign = 0; /* 128 when input negative */
st = 0; /* 16-bit in */
while (fread(&st, 2, 1, stdin) > 0) {
/* Sign */
if (st < 0) {
/* Sign is negative. Limit and change sign. */
if (st < -32767) {
/* This should not happen */
st = -32767;
}
st = st * -1;
sign = 0x80;
} else {
/* Sign is positive. */
sign = 0;
}
/* From 16 to 14 bits */
st = st >> 2;
if (st == 0) {
cnt = 0;
} else if (st < 31) {
/* 1 - 30 */
cnt = 0;
st = (st + 1) / 2;
} else {
/*
* Move 31, 95, 223, 479, 991, 2015 and 4063 to
* 64, 128, 256, 512, 1024, 2048 and 4096.
*/
st = st + 33;
if (st > 8191) {
/* Avoid wrap or overflow */
st = 8191;
}
cnt = 0x10;
/* To 12 bits */
st = st >> 2;
while ((st & 0x0ff0) != 0x10) {
st = st >> 1;
cnt = cnt + 0x10;
/* 112 max */
if(cnt >= 0x70)
break;
}
}
/* Lower 4 bits */
st = st & 0x0f;
/* OR the lot. */
out = sign | cnt | st;
/* XOR with 1111 1111 */
out = out ^ 0xFF;
fwrite(&out, 1, 1, stdout);
}
return(0);
}
There are probably more efficient ways of doing this.
A lot of compression programs use lookup tables.
Decompression
Again, more or less identical to Alaw. However, after the shift we need to subtract 33 (If there is no shift there is no subtraction). And for 8‑bit values smaller than 16, not a '1' but a '0' is appended;
| In | Bits out | Shifts | Min | Max |
|---|---|---|---|---|
| s000abcd | 00000000abcd0 | 0 | 0 | 30 |
| s001abcd | 0000001abcd10 | 1 | 33 | 93 |
| s010abcd | 000001abcd100 | 2 | 99 | 219 |
| s011abcd | 00001abcd1000 | 3 | 231 | 471 |
| s100abcd | 0001abcd10000 | 4 | 495 | 975 |
| s101abcd | 001abcd100000 | 5 | 1023 | 1983 |
| s110abcd | 01abcd1000000 | 6 | 2079 | 3999 |
| s111abcd | 1abcd10000000 | 7 | 4191 | 8031 |
Note: The above min and max values are after subtraction of 33.
In the 'Decompress Alaw' table, the 2nd line isn't shifted;
This one is! Alaw supports six shifts and µlaw seven.
The above output data is 14‑bit. For 16‑bit data, multiply min
and max by 4. So the full 16‑bit output range is 0 to 32124. Or,
including negative numbers, -32124 to 32124. This is about 0.4% less than
Alaw (-32256 to 32256).
A complete µlaw conversion table here.
Alaw VS µlaw
The next graph shows the the result of converting back to 16‑bit.
The graph shows the -16 to 160 range. In the range -123 to 123 the resolution
of µlaw is twice that of Alaw, steps of eight vs 16;
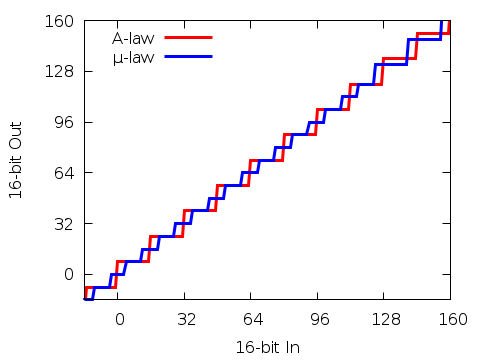
Note that there is no zero in Alaw: It jumps from -8 to 8!
Clearly µlaw has a higher resolution than Alaw for small signals. This at
the expense of slightly larger signals though;
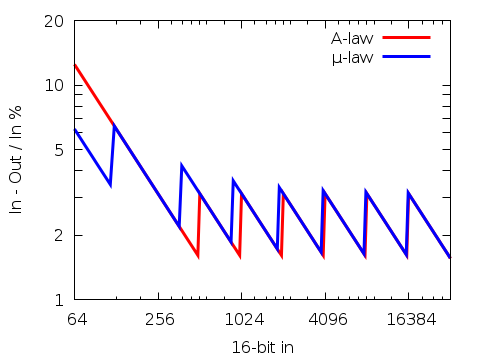
The graph above shows the range from 64 to 32767 with logarithmic scales.
It shows how much the decompressed signal deviates from the the original
before compression expressed as a percentage;
(Original - Decompressed) / Original * 100 percent (actually it's the
'envelope' thereof). When dealing with HiFi audio equipment, this usually
is referred to as distortion.
Each 'jump' in the graph corresponds to a shift; Six for Alaw and seven for
µlaw. For Alaw these are at powers of two: 512, 1024, 2048, etc. µlaw starts
one power earlier and with an offset of -132; 256 - 132 = 124. So that's
124, 380, 892, 1916, etc.
Note: Other documents may refer to this deviation as noise. In which case
the deviation is expressed in dB instead of percent. These graphs are more
or less an upside down version of the graph above.
For values below 124 µlaw performs better. For values larger than 379
Alaw. These are 0.38% and 1.6% of the full range.
µlaw does have a slightly higher dynamic range though. But since a lot of
phones have some sort of automatic gain control, I'm not quite sure how
important a higher dynamic range is.
Note: Some documents define the Alaw and µlaw dynamic range as the highest
value in the highest chord / the highest value in the lowest chord. This
yields 48 dB for µlaw and 42 dB for Alaw.
Links
- G.711
- Digital Telephony (pdf, requires scripting)